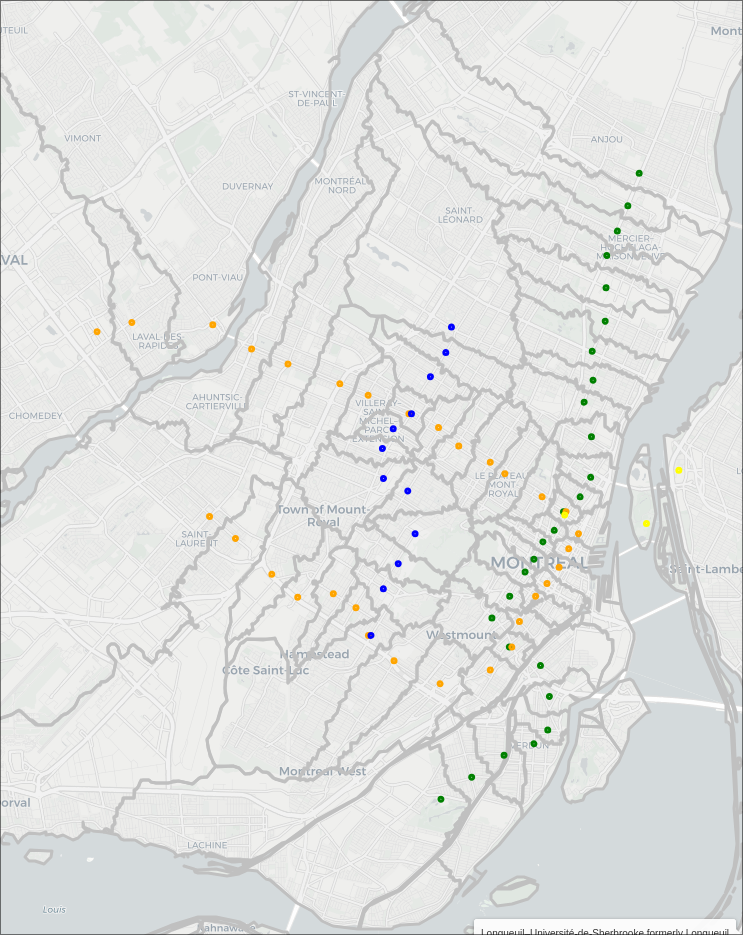
Montreal Metro Walking Map

It started with a simple question. If I'm in a particular location, which metro station is the fastest for me to walk to? Not necessarily the closest in distance, or the one that optimizes my travel time to a final destination. Sometimes, it's really cold out, and you just want to be on the metro asap.

Turns out, you can figure it out, and it's a fun data scraping and analysis problem.

The Map

Interactive version here. Source code badly managed here.

Getting the Data

So there's a few things we need to solve this problem:

• Walking map data for the region of interest
• Location of metro stations
• Shape data of the region of interest, for nice presentation

Remarkably, each of these things is obtainable over the web. I'm really starting to think this internet thing is gonna take off one day.

Walking map data

Thanks to the great work of the OpenStreeMap community, it's super easy to download a huge area of data. I used bbbike's section download to grab the area of montreal, which comes as a compressed osm.pbf file.

From there, we can use pyroutelib3 to read the data, and find shortest routes between locations. Since we're interested in walking distances, we use the FootProfile() to restrict us to footpaths.

import pyroutelib3
from pyroutelib3 import find_route, haversine_earth_distance

with open('Montreal.osm.pbf', "rb") as f:
    graph = pyroutelib3.osm.Graph.from_file(pyroutelib3.osm.FootProfile(), f)

Now as this code suggests, the data is stored as a graph. So, there's a bunch of nodes representing locations, and edges which indicate paths between nodes, and the distance between them. Since we're walking, one way directions don't apply.

Metro station coordinates

Thankfull wikipedia maintains a list of montreal metro stations, with each name linking to a given station's page (e.g. Angrignon) which includes a table containing the coordinates of the station. Now as far as I can tell, the given coordinates represent something like the middle of the platform, and not the coordinates of the actual ground level entrances. So, our walking distances may be off by several meters/minutes, as some of the stations have entrances far from the acutal platform.

I've yet to find a handy list of station entrance coordinates, but the following method could easily be adapted to multiple entrances per station, allowing for a more refined map.

From a specific link to a station page, we can get the coordinates from the page using Beautiful Soup, the html parser:

from bs4 import BeautifulSoup

def get_coords(link):
  base_url = 'https://en.wikipedia.org'
  r = requests.get(base_url + link)
  soup = BeautifulSoup(r.text, 'html.parser')
  coordstring = soup.find(class_="geo").text.strip()
  tuplestring = tuple(map(float, coordstring.split(';')))
  return (tuplestring[1], tuplestring[0])

We can then go over our list of stations, parsing them in a similar maner, and storing all the corodinates:

url = "https://en.wikipedia.org/wiki/List_of_Montreal_Metro_stations"
stations = pd.read_html(url)[1]
response = requests.get(url)
soup = BeautifulSoup(response.text, 'html.parser')
table = soup.find_all('table')[1]
links = []
for tr in table.findAll("tr"):
  trs = tr.findAll("th")
for each in trs:
    try:
    link = each.find('a')['href']
    links.append(link)
    except:
    pass
stations['Link']=links[1:]
stations['coords'] = stations['Link'].apply(get_coords)

Took a bit of trial and error to get the right table sections, this could probably be done in a more clever and robust way by looking of the names of the headers. If you look through the full sourcecode, you'll note that this section is wrapped in some code that caches the results, to avoid pinging wikipedia every time we rerun things.

We now end up with a dattaframe with each entry looking something like

The "Line" entry in the wiki table contains an image that links to the respective stations line. This is difficult to parse, so I just manuually added the line data for each station, using the table order to my advantage:

# Set the line colour of each station
stations.loc[:26,'color'] = 'green'
stations.loc[27:55, 'color'] = 'orange'
stations.loc[56:57, 'color'] = 'yellow'
stations.loc[58:,'color'] = 'blue'

stations.loc[stations[stations['Name'] == 'Berri–UQAM formerly Berri-de Montigny'].index[0],'color2'] = 'orange'
stations.loc[stations[stations['Name'] == 'Berri–UQAM formerly Berri-de Montigny'].index[0],'color3'] = 'yellow'
stations.loc[stations[stations['Name'] == 'Lionel-Groulx'].index[0],'color2'] = 'orange'
stations.loc[stations[stations['Name'] == 'Snowdon'].index[0],'color2'] = 'blue'
stations.loc[stations[stations['Name'] == 'Jean-Talon'].index[0],'color2'] = 'blue'

Note some stations have multiple lines and require special attention.

Now, since our map data is a series of nodes represeting coordinates, it's possible that the station coordinates don't overlap perfectly with a node. Thankfull, we can locate the nearest node to a set of coordinates, though this process is quite slow for the large graph:

nodes = list(map(lambda x: graph.find_nearest_node(x[::-1]),stations['coords']))
stations['node'] = list(map(lambda x: x.id, nodes))
stations['node_coord'] = list(map(lambda x: x.position, nodes))

Seperately we save the node id, and it's corresponding position. Note there's some flipping of the latitude and longitude needed.

Shape Data

Convenitently, the government of canada provides cartographic boundaries for the entire country. This comes as a .shp file which can be read by the geopandas library and manipulated using shapely.

To get the areas we care about, I opted to manualy chose the bounding areas of some of the major islands around montreal, cut them out from the entire country, and then take their convex hull as a large, simple filtering area:

import geopandas as gpd
from shapely import MultiPoint, Point,MultiPolygon,unary_union

# Defining an area of interest based of a roughly rectangular cut of the
# montreal area
canada = gpd.read_file('./lpr_000b16a_e.shp') # Load the shape file
canada = canada.to_crs('WGS84') # Convert to a useable format
quebec = canada[canada['PRENAME'] == 'Quebec'] # Select out quebec
quebecgeo = quebec.iloc[0]['geometry'] # Isolate the geometry

# Use roughly central coordinates to isolate the islands we care about
montreal_lat_lon = (45.514822,-73.582458)
laval_lat_lon = (45.598240,-73.729057)
st_helen_lat_lon = (45.520175,-73.534865)
notre_dame_lat_lon = (45.506991, -73.527333)
longueil_lat_lon = (45.526791, -73.512384)
lat_longs = [montreal_lat_lon,laval_lat_lon,st_helen_lat_lon,notre_dame_lat_lon,longueil_lat_lon]
polygons = []
for lat,lon in lat_longs:
    for poly in quebecgeo.geoms:
        # Find the polygon of quebec that contains the point of interest
        if poly.contains(Point(lon,lat)):
            polygons.append(poly)
# Merge the islands together
islands = MultiPolygon(polygons)

# Set some rectangular bounds
lonmin = -73.75576009950493
lonmax = -73.49785410632529
latmin = 45.412574863304734
latmax = 45.63855628356792
# Cut out square of interest
rect = MultiPoint([(lonmin,latmin),(lonmax,latmax)]).envelope
montrealgeo = quebecgeo.intersection(rect)
islands = islands.intersection(rect)

# Get a rough idea
area = montrealgeo.convex_hull

Visualizing

Combined, we can now use all of this data to start visualizing the problem. Let's start by seeing how close are stations are to their corresponding nearest nodes. Thankfully, geopandas seemlessly works with matplotlib.

While we're at it, we can use the haversine distance between the coordinates to find the maximum error:

# Plot the area with the metro stations and their nearest nodes
fig, ax = plt.subplots(figsize=(12,12))
quebec.plot(ax=ax)
ax.set_xlim(lonmin,lonmax)
ax.set_ylim(latmin,latmax)

errors = []

for i in range(len(stations)):
  d = stations.iloc[i]
  cds = d['coords']
  ncds = d['node_coord']
  ax.plot(cds[0], cds[1],  marker='o', markersize=8,color='C1', zorder=10)
  ax.plot(ncds[1], ncds[0],  marker='o', markersize=8,color='C2', zorder=10)
  errors.append(haversine_earth_distance(cds[::-1],ncds))
print(f"Maximum offset is: {max(errors)*1000:.2f}m")

plt.show()

> Maximum offset is: 32.79m

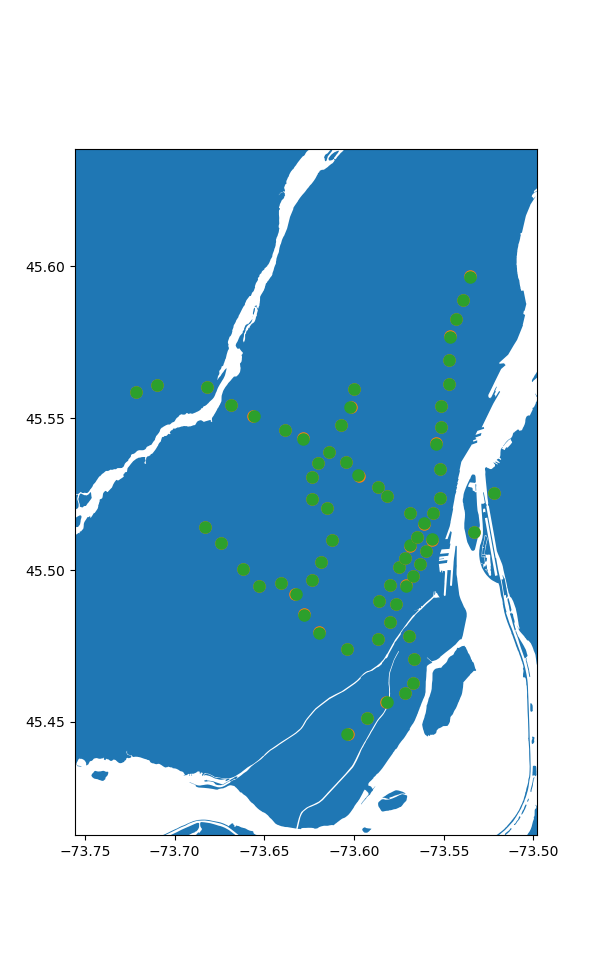
Seems pretty good to me, especially given the caveat between station locations vs their entrances.

Now, to our stations let's add all the map data nodes:

# All together now
fig, ax = plt.subplots(figsize=(12,12))
quebec.plot(ax=ax)
ax.set_xlim(-73.75,-73.472)
ax.set_ylim(45.398,45.623)

lats = []
longs = []
for n,node in graph.nodes.items():
  lats.append(node.position[0])
  longs.append(node.position[1])

ax.scatter(longs, lats,  marker='o', s=8,color='C3', zorder=10)

lats = []
longs = []
# for n in node_stations.keys():
#   loc = router.nodeLatLon(n)
for loc in stations['node_coord']:
  lats.append(loc[0])
  longs.append(loc[1])

ax.scatter(longs, lats,  marker='o', s=8,color='C2', zorder=10)

plt.show()

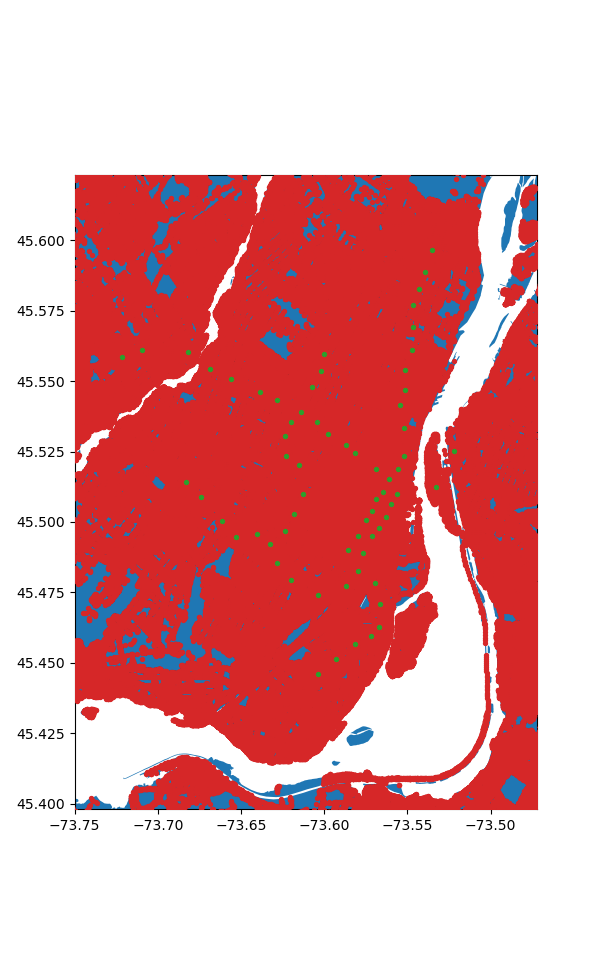
Crunching the Numbers

Okay wow we have a lot of nodes, 1805516 in fact, and 68 stations. Now the most obvious way to solve this problem is easy, for each node we find the shortest path to all the stations and then chose the station with the shortest path. How bad can that be? We only need to compute 122775088 paths. Let's say it takes about a milisecond each since our graph is so big, that puts us at... 1.4 days. Hmm. Ideally it can be faster than that.

If we know a node is closest to a given station, then every node along the path to that station is also closest to that station. But this still requires searching a large number of nodes in a very slow process.

I ended up putting together an algorithm that works backwards, somewhat inspired by floodfill. If we image a liquid oozing out of each station, it will spread outwards, claiming the closest stations before coliding with an other station's fluid. Then we can simply compare the distance to these boundary nodes, as they may have just been checked in a slow order algorithmically, and not actually distance wise. If we claim this node as closer to the later station, we should also check its neighbours and repeat until we run out of nodes to check.

Programatically this looks like keeping a queue of nodes to check for each station, starting from it's nearest nodes neighbours, and performing a breadth first search of nearby nodes, while keeping track of the distance to each node. Then, we iterate over each station until we run out of nodes to check:

s_n_dict = dict(zip(stations['Name'].to_list(),stations['node'].to_list()))
s_n = list(s_n_dict.keys())
# Cache data so we don't need to run the expensive part every time.
filename = "./cached_flood_nodes.json"
nodes_file = Path(filename)
if nodes_file.exists():
    with nodes_file.open('r') as f:
        node_stations = json.load(f)
    for key in list(node_stations.keys()):
        node_stations[int(key)] = node_stations.pop(key)
else:
# Do the computation
    # Start with an empty point of all the nodes in the grpah that are in our area of interest
    # This part is somewhat slow to process, but important for avoiding invalid nodes.
    node_stations = {n:['',np.inf] for n in tqdm(graph.nodes) if area.contains(Point(graph.get_node(n).position[::-1]))}
    for name,node in s_n_dict.items():
        # Claim each metro station's node with its name and zero distance.
        node_stations[node] = (name,0)
    # Initialize the queues with the stations neighbouring nodes
    queues = {n:[(s_n_dict[n],node,0) for node in graph.edges[s_n_dict[n]].keys() if node in node_stations.keys()] for n in s_n}
    iters = 0 # Track our iterations
    # While there's still stations processing
    while len(s_n) > 0:
        # Status update
        print(iters, len(s_n), sum([len(queue) for queue in queues.values()]))
        # Loop over each station
        for i,name in enumerate(s_n):
            # Remove from processing if it has no more elements
            if len(queues[name]) == 0:
                print(s_n.pop(i))
            else:
                # Sort the queued nodes by their distance
                queues[name] = sorted(queues[name],key=lambda x: x[2])
                # Get current length of queue to process
                queue_len = len(queues[name])
                # For each element in queue
                for _ in range(queue_len):
                    # Remove element
                    old_node,new_node,distance = queues[name].pop(0)
                    # Update the total distance to this node
                    total_distance = distance + graph.edges.get(old_node,{}).get(new_node,np.inf)
                    # If the total distance is shorter then currently stored, update it
                    if total_distance < node_stations[new_node][1]:
                        node_stations[new_node] = (name,total_distance)
                        # Then, add each of this nodes neighbours to the queue for consideration
                        # except for the node we're currently at, and any outside of our exclusion zone
                        for node in graph.edges.get(new_node,{}).keys():
                            if node != old_node and node in node_stations.keys():
                                queues[name].append((new_node,node,total_distance))
        iters += 1
    with nodes_file.open('w') as f:
        json.dump(node_stations,f)

Remarkably, this churns through all the nodes in a little under 2 minutes, now that's an improvement! We can do an initial rough visualization by plotting each node, colored according to it's station.

fig, ax = plt.subplots(figsize=(12,12))
quebec.plot(ax=ax,color='gray')
ax.set_xlim(-73.75,-73.472)
ax.set_ylim(45.398,45.623)
from cycler import cycler
dc = cycler(color=['#E8ECFB', '#D9CCE3', '#D1BBD7', '#CAACCB', '#BA8DB4', '#AE76A3',
                   '#AA6F9E', '#994F88', '#882E72', '#1965B0', '#437DBF', '#5289C7',
                   '#6195CF', '#7BAFDE', '#4EB265', '#90C987', '#CAE0AB', '#F7F056',
                   '#F7CB45', '#F6C141', '#F4A736', '#F1932D', '#EE8026', '#E8601C',
                   '#E65518', '#DC050C', '#A5170E', '#72190E', '#42150A'])
names = s_n_dict.keys()
ax.set_prop_cycle(dc)
for name in names:
    lats = []
    longs = []
    for n in node_stations.keys():
        if node_stations[n][0] == name:
            loc = graph.get_node(n).position
            lats.append(loc[0])
            longs.append(loc[1])
    print(name,len(lats))
    ax.scatter(longs, lats,  marker='o', s=8, zorder=10,label=name)
plt.show()

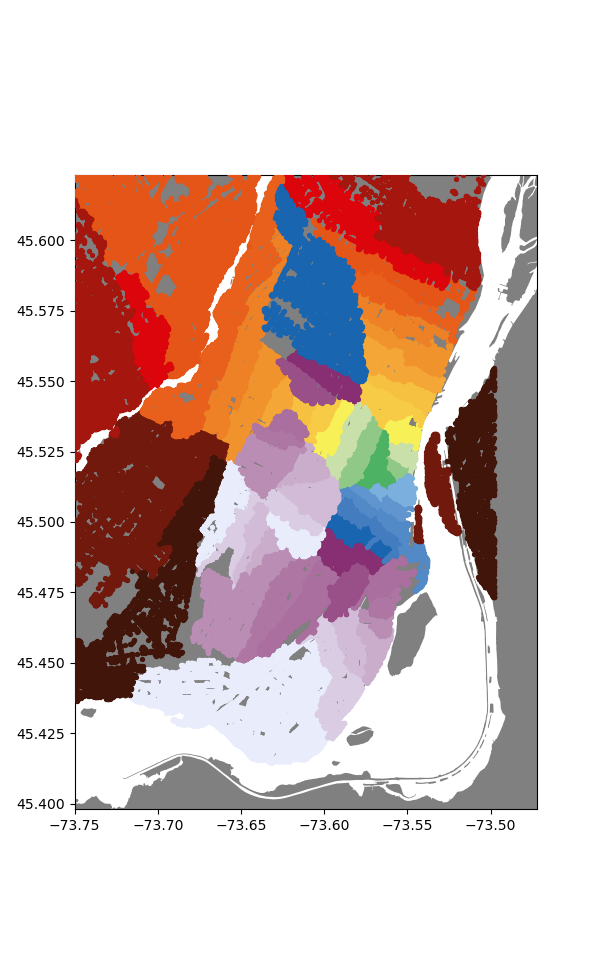
Now already I'm super happy with how this looks, we get nice (mostly) enclosed areas, all somewhat centered on their respective stations. To make this a bit more polished, lets convert these sets of points into distinct regions.

I opted to do this by first inerpolating the whole map data, and then sectioning out the regions for nice mapping.

So, first interpolation:

from scipy.interpolate import NearestNDInterpolator
station_maping = {name:i for i,name in enumerate(s_n_dict.keys())}
rev_station_maping = {i:name for i,name in enumerate(s_n_dict.keys())}


x = []
y = []
for node,station in node_stations.items():
    loc = graph.get_node(node).position
    x.append((loc[1],loc[0]))
    y.append(station_maping.get(station[0],-1))

xs = np.linspace(lonmin,lonmax,3000)
ys = np.linspace(latmin,latmax,3000)
X,Y = np.meshgrid(xs,ys)

x = np.array(x)
y = np.array(y)
idxs = y > -1
x = x[idxs]
y = y[idxs]
interp = NearestNDInterpolator(x,y)
Z = interp(X,Y)

plt.figure()
plt.pcolormesh(X, Y, Z, shading='auto',cmap='flag')
plt.show()

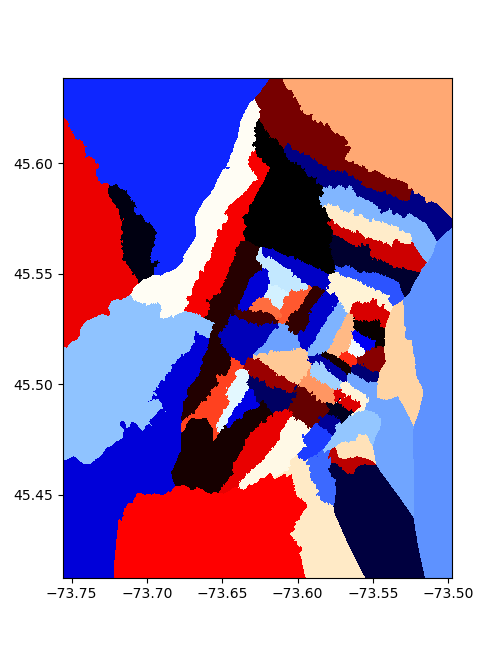
To section the areas, I took each point, and formed a little square around it, then merged all the squares corresponding to one station to make things overlap nicely, we feather/buffer the edges by a value proportional to the typical point spacing:

dx = np.mean(np.diff(xs))
dy = np.mean(np.diff(ys))

value = 0
polys = {value:None for value in set(Z.ravel())}
for value in tqdm(polys.keys()):
    ps = []
    idxs = np.where(Z == value)
    for i,j in zip(idxs[0],idxs[1]):
        if Z[i,j] > -1:
            x = X[i,j]
            y = Y[i,j]
            ps.append(MultiPoint([(x-dx/1.8,y-dy/1.8),(x+dx/1.8,y+dy/1.8)]).envelope)
    polys[value] = unary_union(ps).buffer(-dx*0.2/4).intersection(montrealgeo)
for key in list(polys.keys()):
    polys[rev_station_maping.get(key,'None')] = polys.pop(key)

This is remarkably slow, taking several minutes.

Making the map

With all that done, we can use folium to nicely plot the results on an interactive map. A lot of the code is just adding the station information and circles to represent them.

import folium
m = folium.Map(location=[45.50884, -73.58781], zoom_start=13, tiles='CartoDB positron')
def make_style(color):
  return lambda x: {'color' : color}

for name, poly in polys.items():
  name = name
  popup = f'{name} Station'
  color = stations[stations['Name']==name].values[0][-1]
  # geo_j = folium.GeoJson(data=poly, style_function=make_style(color), tooltip = name)
  geo_j = folium.GeoJson(data=poly, style_function=lambda x: {'color':'silver'}, tooltip = name)
  folium.Popup(popup).add_to(geo_j)
  geo_j.add_to(m)
as linked above, or again here
scale = 5
for i in range(len(stations)):
  d = stations.iloc[i]
  cds = d['coords']
  name = d['Name']
  col = [c for c in [d['color'],d['color2'],d['color3']] if isinstance(c,str)]

  if len(col) == 1:
    folium.Circle(
      radius=50,
      location=[cds[1], cds[0]],
      popup = name,
      color = col,
      fill=True,
      tooltip = name).add_to(m)
  elif len(col) == 2:
    folium.Circle(
    radius=50,
    location=[cds[1], cds[0]-scale*dx],
    popup = name,
    color = col[0],
    fill=True,
    tooltip = name).add_to(m)

    folium.Circle(
    radius=50,
    location=[cds[1], cds[0]+scale*dx],
    popup = name,
    color = col[1],
    fill=True,
    tooltip = name).add_to(m)
  elif len(col) == 3:
    folium.Circle(
    radius=50,
    location=[cds[1], cds[0]-scale*dx],
    popup = name,
    color = col[0],
    fill=True,
    tooltip = name).add_to(m)

    folium.Circle(
    radius=50,
    location=[cds[1], cds[0]+scale*dx],
    popup = name,
    color = col[1],
    fill=True,
    tooltip = name).add_to(m)

    folium.Circle(
    radius=50,
    location=[cds[1]-2*scale*dy, cds[0]],
    popup = name,
    color = col[2],
    fill=True,
    tooltip = name).add_to(m)

This then gets saved out as an html file, which was linked at the start, or again here.

Some interesting points

Overall I'm happy with the turnout of the map. That being said, there are definitely some issues. The original attempt had a few stations with very small areas, that we're clearly not propagating out properly. At first I thought this was an issue with the algorithm. Turns out, as always in montreal, there was construction around these stations, and so the were on isolated islands in the graph data from OSM. So I fudged their coordinates a bit to get the presented results. Similar issues seem to plague all recent datasets I've tried to download. Gotta love this city...

Additionally, there are some funny artifacts on parts of the map e.g.:

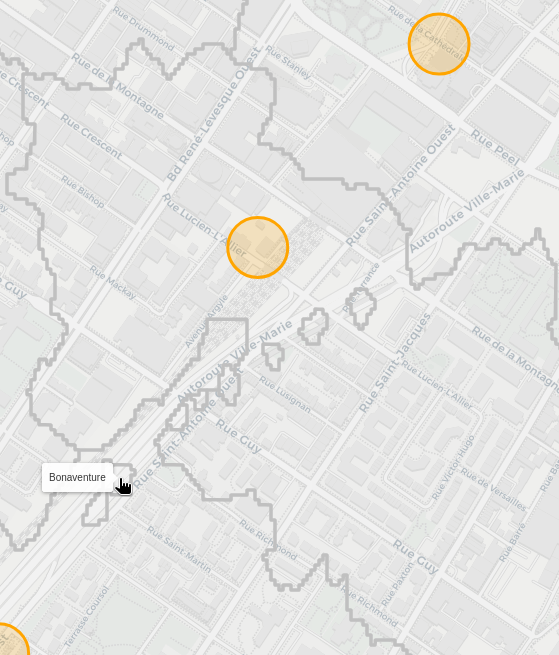
Boneaventure station is clearly spilling out into its neighbouring areas of Lucien-L'Allier and Georges-Vanier. From what I can tell, this occurs if you're walking on the Ville-Marie autoroute, as the nearest pedestrian entrance brings you into the capture area of bonaventure. Now I'm not sure if you can even actually walk there, so I need to check if I'm correctly parsing the OSM data to only accept places you can walk.

There's other similar blobs that are actually correct though, like this section where berri steals a bit from sherbrooke:

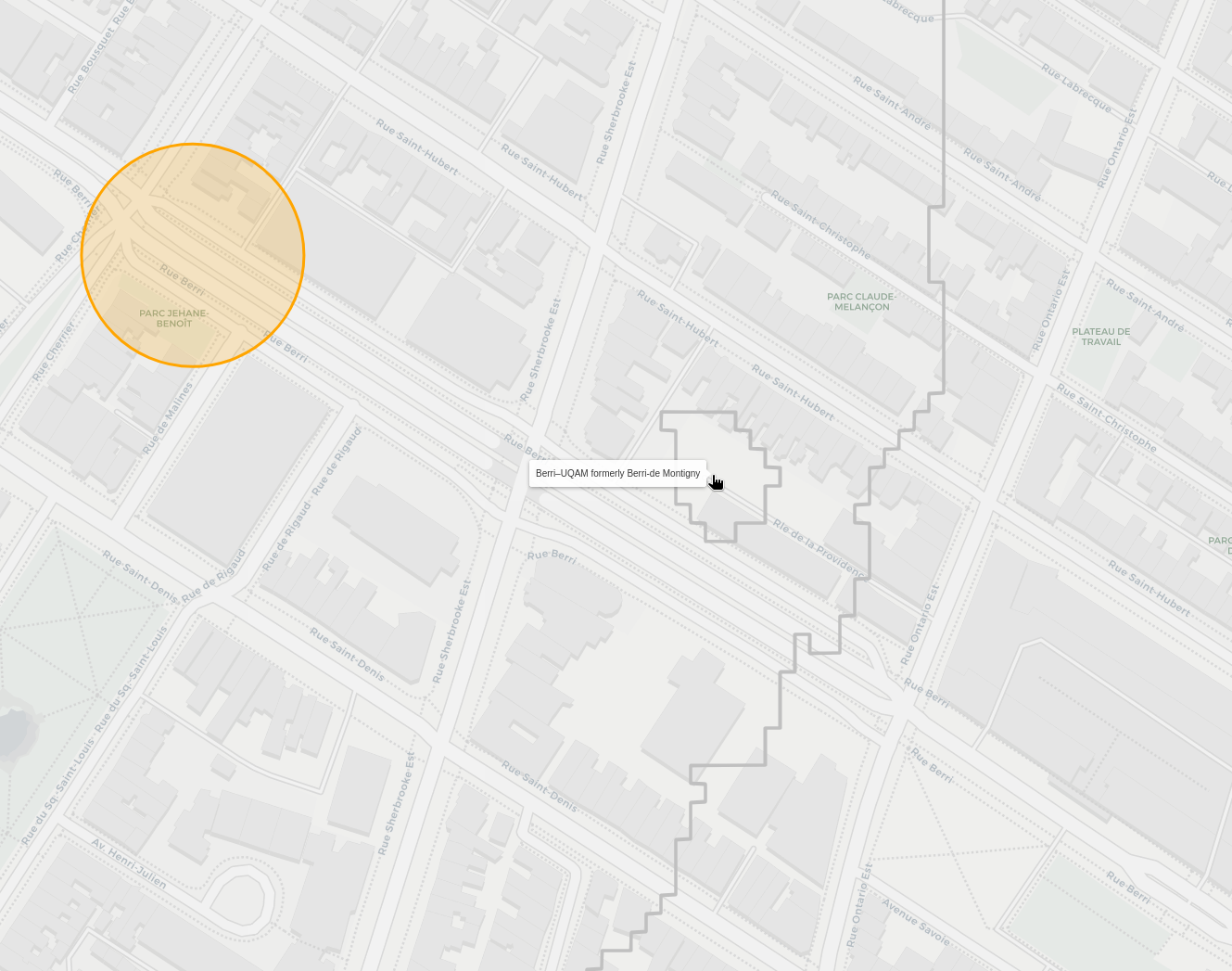
Since there's an alley, if you're at the tip of it, you need to walk back down to a section that is closer to Berrie. The issue here is how I'm interpolating and selecting the regions. Since there's no node halfway through the alley, it ends up being closer to the sherbrooke sections in the interpolation. Close enough for now I think.

Now personally, I used to live near the corner of St-Urbain and Bagg, and I always felt like I had three equal options of stations to walk through, but typicall went to Sherbrooke, as it felt a little closer. Surely enough, looking at our results, I was very close to a three way border:

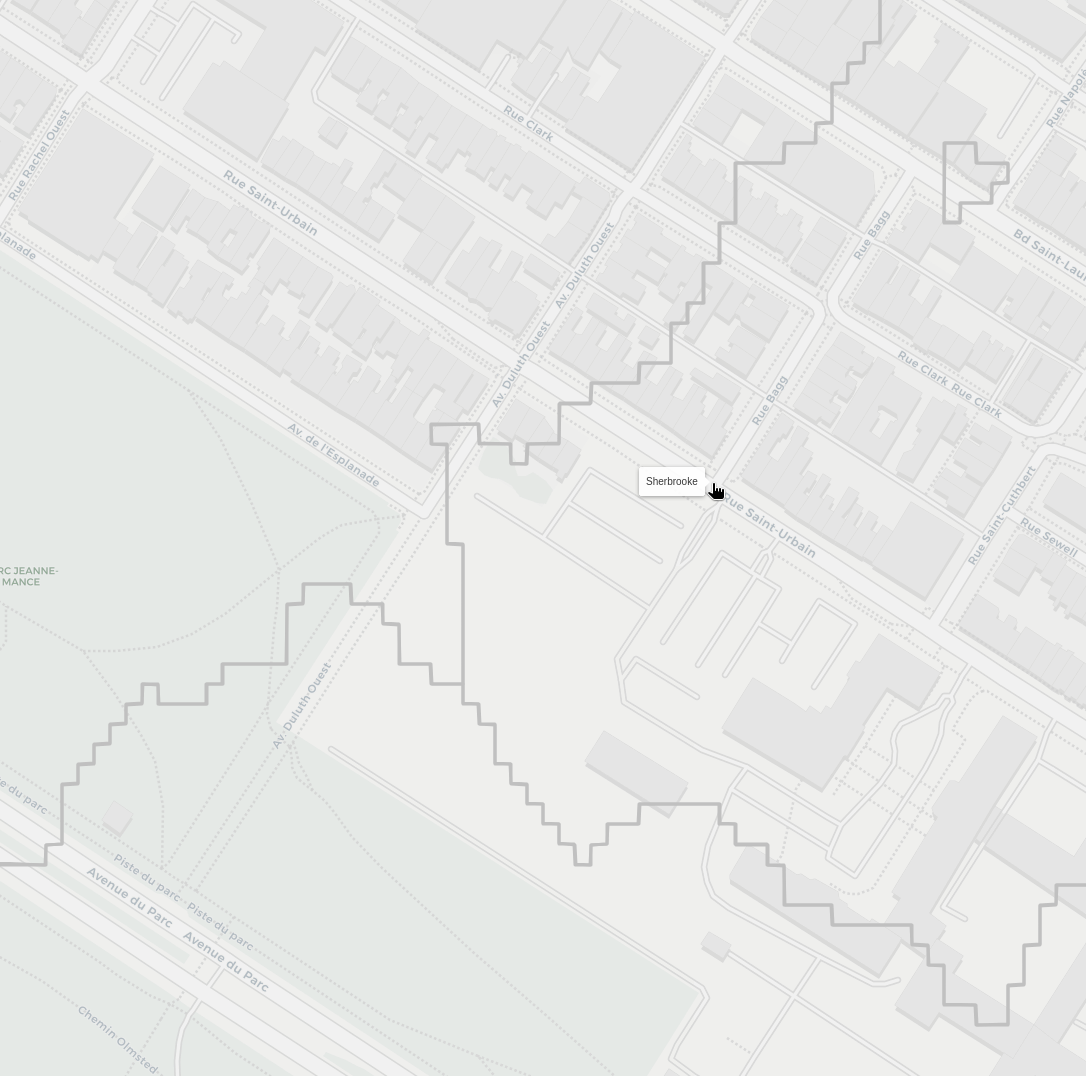
Though, it seems like my intuition for Sherbrooke being slightly closer was correct!

That screenshot also contains an other alley caused artefact, though this one looks like it has signifncant mismatch between the node position and where it is on the map. So there's definitely some refining to do.

Perhaps one day I'll get this working better, but for now I'm happy with the results, thanks for coming on this adventure with me, I hope the map can be useful for some of you!